[Complete Guide] Creating MATLAB Matrix | Mathematical Operations and Functions

If you look at the MATLAB, Vector and Matrix are two basic fundamentals components. So, we need to become familiar with the matrix, vector, how to generate them, different MATLAB matrix operations and functions…

In the last tutorial, I described the MATLAB Vector with their functions and mathematical manipulations on the MATLAB command window. 

Let’s start this complete tutorial about MATLAB matrix operations.

Table of Content:

• Introduction about the Matrix in MATLAB
• Creating and Generating the Matrix in MATLAB 
• Transpos of the Matrix
• Determinant of the Matrix
• Inverse of the Matrix
• MATLAB Matrix Operation
• Matrix Functions in MATLAB
• • Getting all Diagonal Elements of the Matrix
  • Finding out Eigenvalue of the Matrix
  • Determining the Rank of the Matrix
  • Creating a Zero Matrix
  • Generating an Identity Matrix
  • Creating a Ones Matrix
  • Finding a Size of the Matrix

INTRODUCTION

The definition of the Matrix is a two-dimensional array which consists of both the rows and columns. 

In the MATLAB matrix, the rows and columns are created by using the commas (,) / line-spaces (  ) and semicolon (;) respectively. 

The matric is represented by the square brackets ‘[ ]’.

Creating and Generating the Matrix in MATLAB 

In the generation of the matrix section, we are studying ‘How to create the Matrix [Rows and Columns] in MATLAB?’. 

The last tutorials I shared ‘How to create the vector in MATLAB?’. This tutorial is about creating the Matrix rows and columns with the detail explanation. 

For creating MATLAB Matrix, you must have four points to remember. 

• Start with the open square bracket ‘[‘
• Create the rows in the matrix by using the commas (,) or line-spaces ( )
• Create the columns in the matrix by using the semi-colon ( ; )
• End with the close square bracket ‘]’

Let’s look at the general representation of matrix with the row and column…

The general representation of Row Matrix is…

A = [x1, x2, x3, ....... xn] or [x1 x2 x3 ....... xn]

This is (1 × n) vector i.e. a single row consisting the n th term elements.

The general representation of Column Matrix is…

A = [x1; x2; x3; ....... xm] 

This is (m × 1) vector i.e. a single row consisting the m th term elements.

Note: Row matrix and column matrix are nothing but the vectors.

For example, 

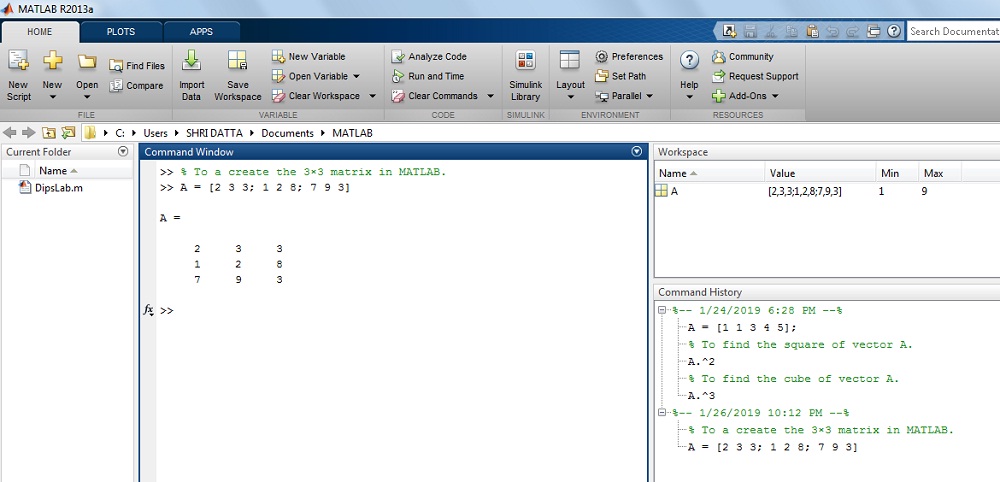
How to generate or create N×M Matrix in MATLAB?

Solution:  The 3×3 matrix must have 3 rows and 3 columns. These rows and columns are created with the help of space and semicolon.

The matrix in MATLAB: 

>> Matrix A is...

>> A= [2 3 3; 1 2 8; 7 9 3]

A = 

       2   3    3

       1   2    8 

       7   9    3

The output on MATLAB Window:

In this section, we have seen how to create and generate the matrix.

Moving to the next part…

TRANSPOSING OF MATRIX

What is the Transpose of the Matrix?

Transpose method is a mathematical operation where…

• The elements of the row are converted into the elements of the column. (or)
• The elements of the column are converted into the elements of the row.

The transpose of the Matrix is represented by an apostrophe or single quote (‘) or power of T like as [ ]’ 0r [ ]T.

Note: The representation of the transpose of the Matrix is the same as the representation of the transpose of the vector. 

Here is a general syntax for Transpose of the Matrix.

Transpose of matrix A (A’) is

A = [x1 x2 x3; x4 x5 x6; x7 x8 x9]'= [x1 x4 x7; x2 x5 x8; x3 x6 x9] 

Transpose of matrix B (B’) is

B = [x1 x4 x7; x2 x5 x8; x3 x6 x9]' = [x1 x2 x3; x4 x5 x6; x7 x8 x9]

If you perform transpose operation twice on the matrix, it will give the same matrix.

i.e.

A = (A')'

Let’s take a mathematics example…

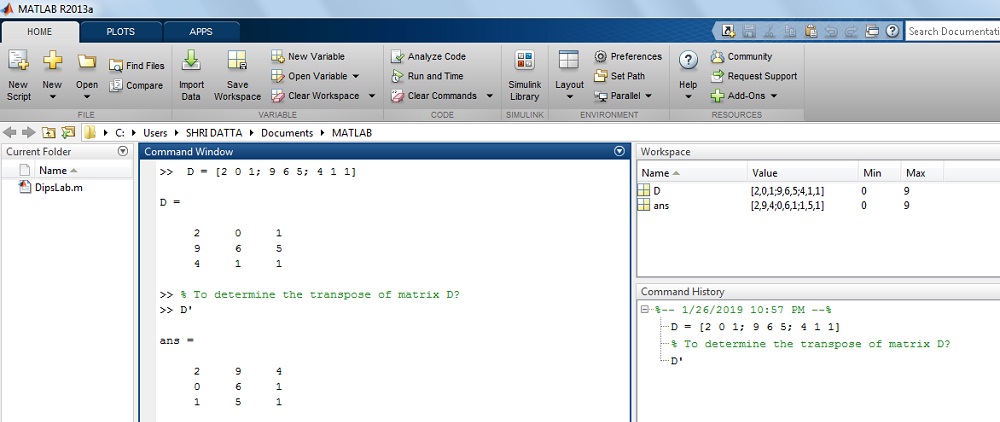
How to determine the transpose of the given below matrix D?

where D = [2 0 1; 9 6 8; 4 1 1]

Solution: You can use the transpose method to change the row vector into a column vector.

>> D = 
         2   0   1

         9   6   8

         4   1   1

>> By using the transpose method,

>> D' =
         2   9   4

         0   6   1

         1   8   1

The output on the MATLAB Window:

Looks like its pretty simple till now. Isn’t it?

DETERMINANT OF MATRIX

What is a determinant of the Matrix?

It is a special number calculated from the square matrix. If you are not aware of determinant if the matrix, you can check here.

Note: You can calculate the matrix determinant only where if it is square matrix means the number of rows and the number of columns will be the same.

In MATLAB, we can easily determine the ‘Determinant of Matrix’ by using the ‘det’ function. You don’t need to do any mathematical operation explicitly.

The general Syntax is, 

x = det(x) Return the determinant of matrix 'x'

Where, x is matrix. 

Example,

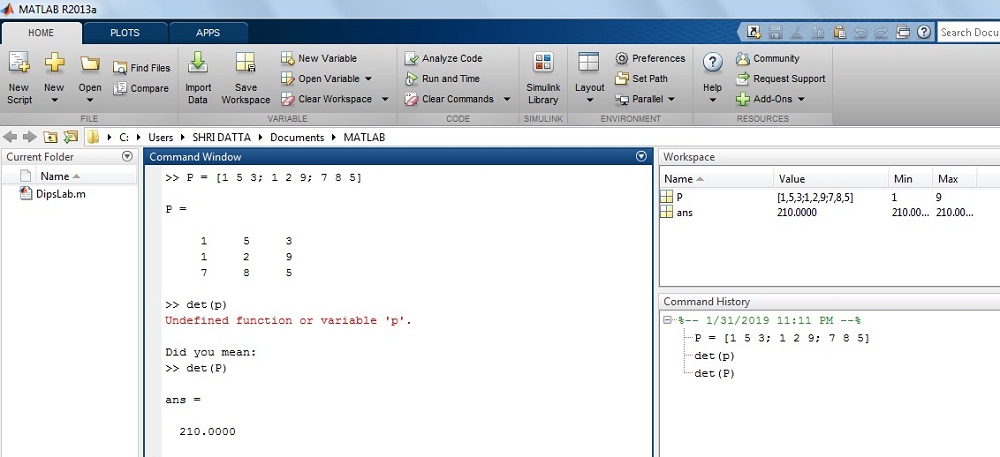
How to find the determinate of matrix ‘P’ in MATLAB?

Where, P = [1 5 3; 1 2 9; 7 8 5]

Solution: The given value of matrix ‘P’ is

>> P = [1 5 3; 1 2 9; 7 8 5]
>> P = 

       1   5   3

       1   2   9

       7   8   5

>> det(P)

ans    = 
       210.0000

The output on MATLAB Window:

INVERSE OF MATRIX

What is Inverse of the Matrix?

If the multiplication of the matrix A and matrix B is the Identity matrix, matrix B is the inverse of matrix A.

If you are interested to know how to calculate the inverse of matrix mathematically, check this link.

In MATLAB, the inverse of the matrix is calculating by using the ‘inv’ function. The representation of inverse matrix is ‘matrix power of -1’ or []-1

The general Syntax is…

x = inv(x) Return the inverse value of matrix 'x'

Where, x is matrix. 

Example.

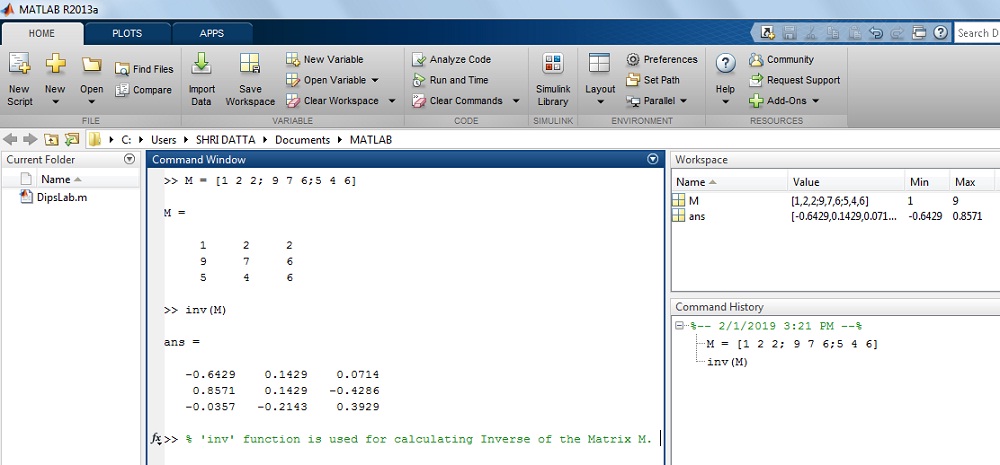
How to calculate the inverse of the matrix M in MATLAB?

Where, M=[1 2 2; 9 7 6; 5 4 6]

Solution: By using the inverse function, 

>> M=[1 2 2; 9 7 6; 5 4 6]

>> M= 

     1   2   2

     9   7   6
 
     5   4   6

>> inv(M)

ans  =
       -0.6429   0.1429   0.0714
        0.8571   0.1429  -0.4286
       -0.0357  -0.2143   0.3929

The output on MATLAB Window:

This is all about a simple function to calculate the inverse of the matrix in MATLAB. 

MATLAB MATRIX OPERATIONS [Mathematical]

Earlier we have seen the different types of mathematical functions and their short abbreviations. In this section, we will perform same mathematical operations on Matrix.

In the MATLAB environment, the mathematical operations (functions) on Matrix are the same as Vector. 

What are the different mathematical operations we can perform on the matrix in MATLAB?

Mathematical Arithmetic Operation	Notation andSyntax for Matrix
Addition	+
Subtraction	–
Multiplication	.*
Division	./
Exponential or power	.^

MATRIX FUNCTIONS in MATLAB

The MATLAB provides the various functions for mathematical matrix manipulation.

We will see those MATLAB matrix functions one by one…

1. How to find Diagonal element of the Matrix in MATLAB?

In the MATLAB command window, ‘diag’ syntax is used to get the diagonal elements of the matrix. 

The general Syntax:

x = diag(x) Return the diagonal value of matrix 'x'

Where, x is matrix. 

Example

How to get all the diagonal elements of Matrix B in MATLAB?

Where, B = [2 3 4; 1 1 9; 2 7 8]

Solution: The given value of matrix B is

>> B = [2 3 4; 1 1 9; 2 7 8]

>> B = 

           2    3    4

           1    1    9
 
           2    7    8


>> diag(B)

ans =
      2
      1
      8

The result on MATLAB display:

2. How to determine the Eigen-value of the Matrix in MATLAB?

What is Eigen-Value of Matrix and how to calculate it?

Note: This video is just for your understanding.  You don’t need to do any mathematical operations to find the eigenvalue of the matrix in MATLAB.

In MATLAB, it is pretty easy.

The eigenvalue of the matrix calculated by using the ‘eig’ syntax in MATLAB.

The general Syntax is, 

x = eig(x) Return the eigen value of matrix 'x'

Where, x is matrix.

Example.

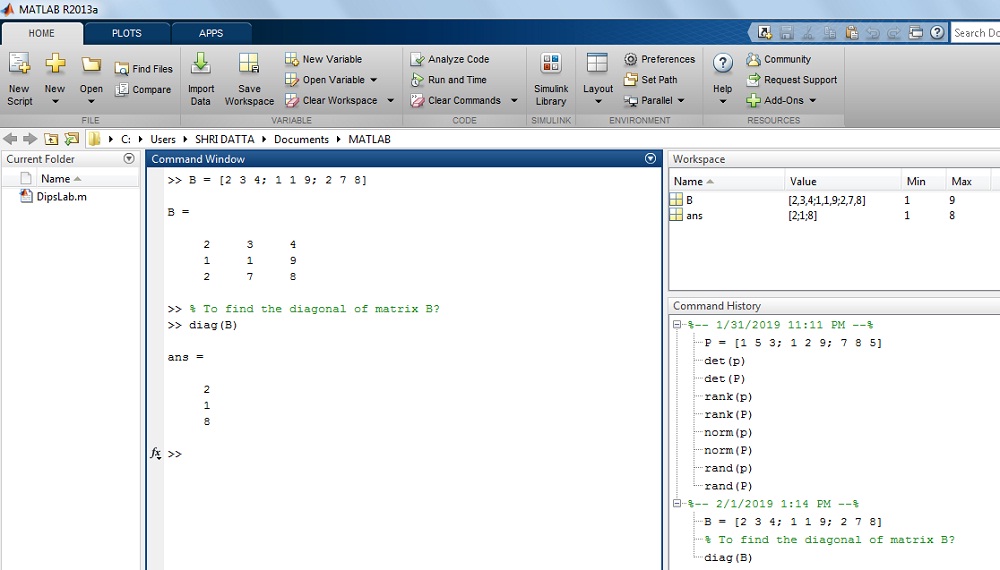
How to find the eigenvalue of Matrix B in MATLAB?

Where, B = [2 3 4; 1 1 9; 2 7 8]

Solution:

>> B = [2 3 4; 1 1 9; 2 7 8]

>> B = 

           2    3   4

           1    1    9

           2    7    8
ans =

      14.1021

      1.0297

     -4.1318

 The result on MATLAB display:

3. How to find the Rank of the Matrix in MATLAB?

What is the rank of the matrix?

The rank of a matrix is defined as the maximum number of linearly independent column vectors in the matrix. It is similar to the maximum number of linearly independent row vectors in the given matrix.

Here is video if you are interested in finding rank of the matrix in general.

In MATLAB to find the Rank matrix, ‘rank’ function is used. 

The general Syntax is..

x = rank(x) Return the rank of matrix 'x'

Where, x is matrix. 

Example.

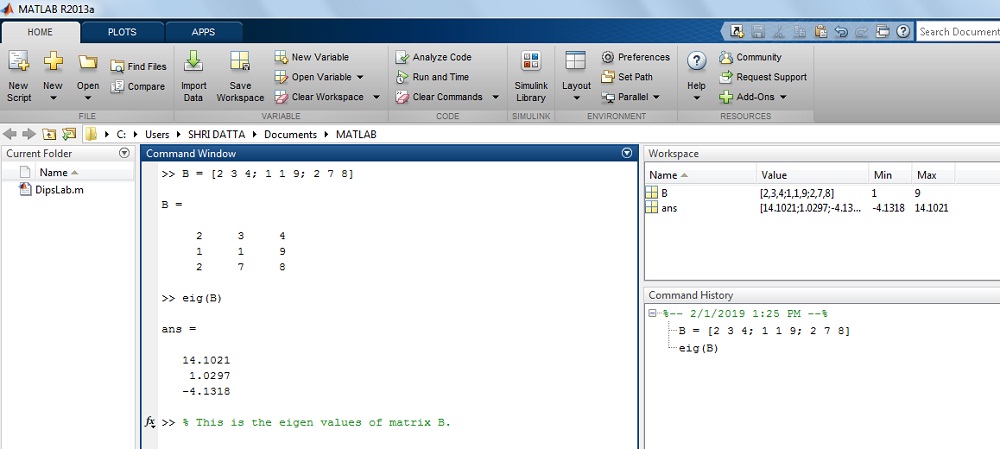
How to find out the rank of Matrix B in MATLAB?

Where, B = [2 3 4; 1 1 9; 2 7 8]

Solution: For the given matrix B, 

>> B = [2 3 4; 1 1 9; 2 7 8]

>> B = 

           2    3   4

           1    1    9

           2    7    8

>>rank(B)

ans = 
      3

The result on MATLAB display:

4. How to create Zero Matrix using zeros function in MATLAB?

What is Zero Matrix?

In the zero matrix, all the elements of the matrix are zero. 

In the case of MATLAB, zeros function is used to create all zero in rows and columns of the matrix.

The general Syntax is…

x = zeros(x) Return the zeros of matrix 'x'

Where, x is matrix. 

Example.

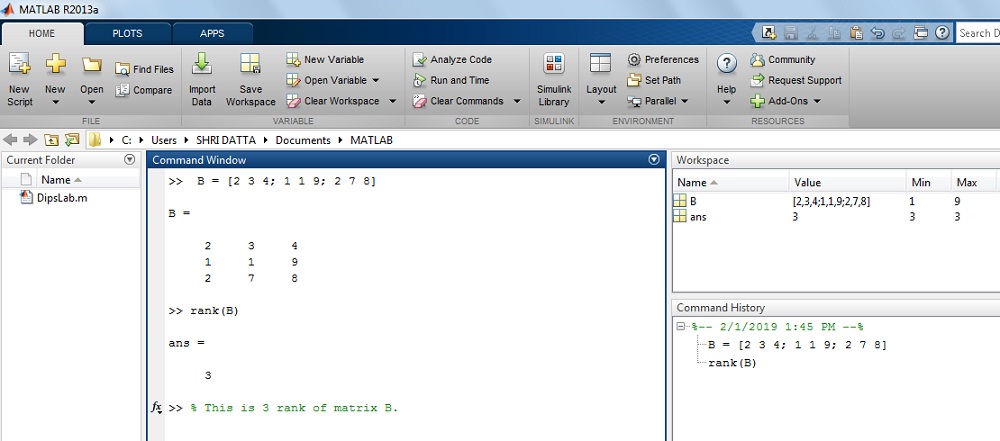
How to create a zero matrix in MATLAB? 

Where, matrix A is 3 by 2 matrix,

Solution: The matrix A is

>> A= zeros(3,2)

ans  =

       0   0
       0   0
       0   0

The result on MATLAB display:

5. How to create Identity matrix using eye Function in MATLAB?

 The eyes function in MATLAB is used to create the identity matrix.

The general Syntax is… 

x = eye(x) Return the eye of matrix 'x'

Where, x is matrix. 

Example.

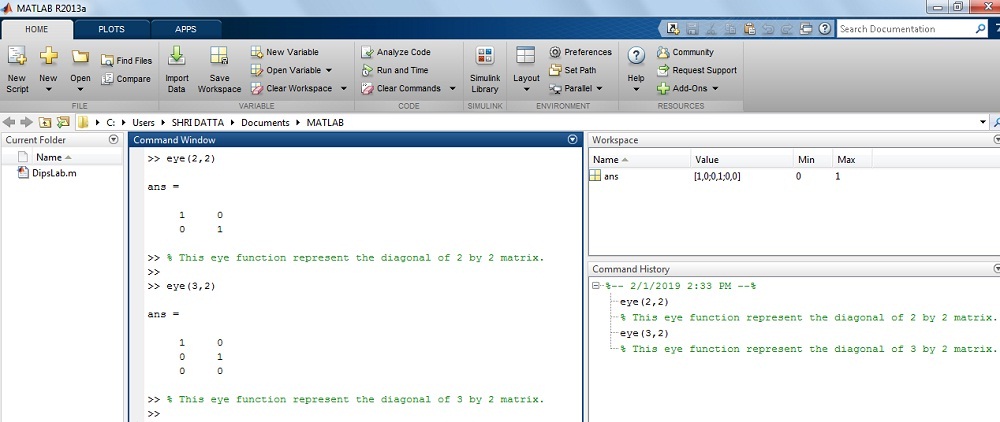
How to generate the Identify Matrix by using the eye function in MATLAB?

Where matrix A is 2 by 2 matrix.

Solution: The matrix A is…

>> eye(2,2)

ans =

       1  0

       0  1

The result on MATLAB display:

6. How to create Matrix with all elements as one using ones function in MATLAB

In MATLAB, the ‘ones’ function is useful for creating the matrix with all elements one. 

The general Syntax is… 

x = ones(a) Return the ones of matrix 'x'

Where, 'a' is a size of the matrix

Example.

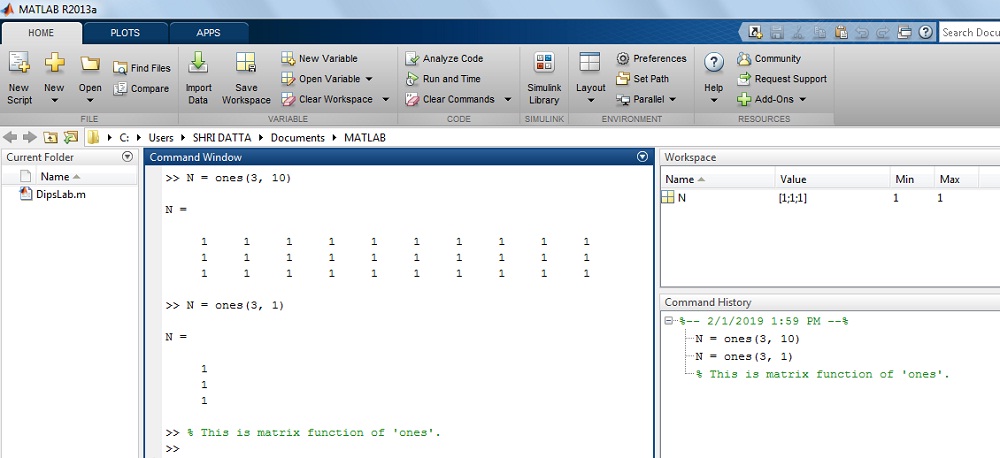
How to generate  the matrix with all elements one in MATLAB?

Where, matrix A is 2 by 2.

Solution:

>> A = ones(2)

ans =

       1  1

      1   1

Or

>> N = ones(3,1)
N =
1 
1
1

The result on MATLAB display:

7. How to find the size of the matrix in MATLAB?

In MATLAB, we can find out the number of columns and rows with the help of ‘size’ function. 

The general Syntax is, 

s = size(x) Return the size of matrix 'x'

Where, x is matrix.

Example,

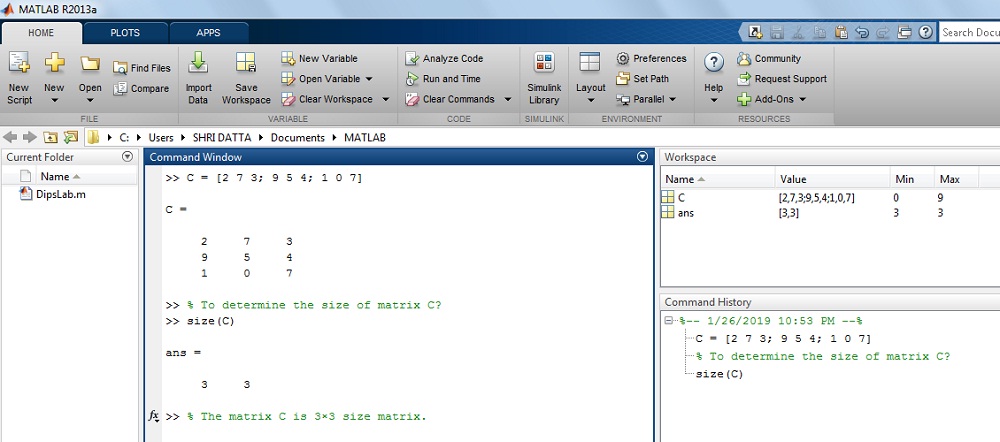
How to determine the size of matrix C in MATLAB?

Where, C = [2 7 3; 9 5 4; 1 0 7]

Solution: The given value of matrix C,

>> C = [2 7 3; 9 5 4; 1 0 7]

>> C =

       2   7   3

       9   5   4

       1   0   7


>> size(C)

ans = 
      3   3

The result on MATLAB display:

On this Matrix MATLAB tutorial, I tied my best covering all the basics of the matrix. And also explained mathematical operations and functions of the matrix by solving examples on the command window of MATLAB Software. 

Check my all other MATLAB tutorials and keep exploring. I will be sharing more of such tutorials, stay tuned.

If you have any query related to different MATLAB matrix operations, feel free to ask by commenting below. If you like this tutorial please comment your feedback and also share it with your friends and students.